Bonjour.
1 - Constitution de l'oscillateur gravitationnelle:
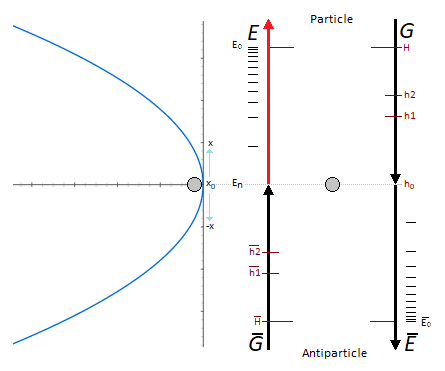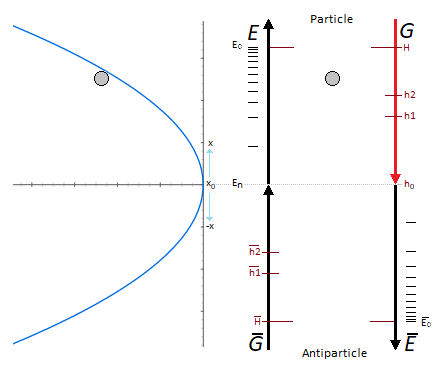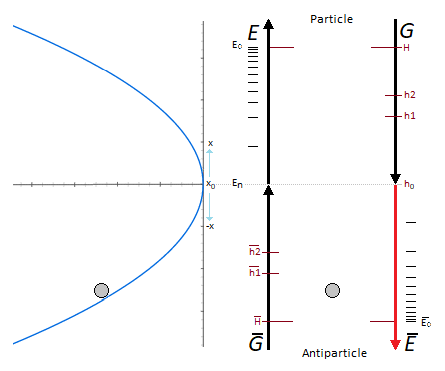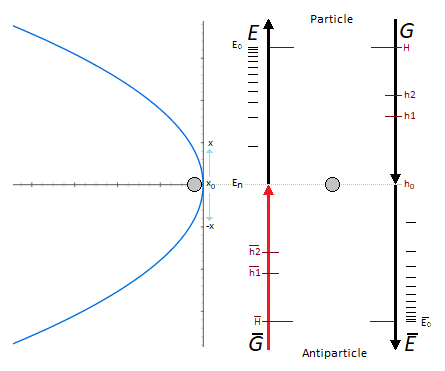
Cet oscillateur linéaire utilise une particule de masse m oscillant à la verticale suivant le vecteur G de la gravité.
L'oscillation comprend deux phases. La première est la phase de la chute de la particule avec la force G, et la seconde est la phase inverse qui correspond à l'éjection verticale de la particule donnée par une impulsion d'énergie E. Oscillation montante de la particule = E , oscillation descendante de la particule = G.

La gravité est de l'énergie, mais inverse pour E dans notre cas de figure.
E - G = 0
Quantité de mouvement de la particule dans l'oscillateur:

Vitesse et accélération de la constante g de la particule:

2 - Principe d'incertitude d'Heisenberg
L'intégration de la constante g se fait avec le principe d'incertitude d'Heisenberg:
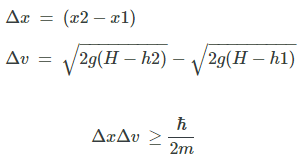
Quantité de mouvement k donnée à la particule après l'impulsion:
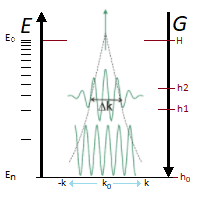
États cohérents d'un oscillateur et principe d'incertitude:

3 - Électron et vitesse de la lumière:
La gravité quantique nommée z ferait alors tomber la particule de la surface, pour ensuite réapparaître grâce à l'énergie. Autant la constante g a une accélération sur un objet relativiste, alors z serait une constante d'accélération de la particule quantique pour atteindre la vitesse de la lumière.
Nous pouvons déterminer la quantité d'énergie qu'il faudrait pour déplacer l'électron à c-1:

Énergie potentielle gravitationnelle quantique de l'électron et constante z :

1 - Constitution de l'oscillateur gravitationnelle:
Cet oscillateur linéaire utilise une particule de masse m oscillant à la verticale suivant le vecteur G de la gravité.
L'oscillation comprend deux phases. La première est la phase de la chute de la particule avec la force G, et la seconde est la phase inverse qui correspond à l'éjection verticale de la particule donnée par une impulsion d'énergie E. Oscillation montante de la particule = E , oscillation descendante de la particule = G.

La gravité est de l'énergie, mais inverse pour E dans notre cas de figure.
E - G = 0
Quantité de mouvement de la particule dans l'oscillateur:

Vitesse et accélération de la constante g de la particule:

2 - Principe d'incertitude d'Heisenberg
L'intégration de la constante g se fait avec le principe d'incertitude d'Heisenberg:
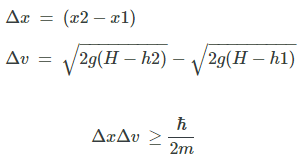
Quantité de mouvement k donnée à la particule après l'impulsion:

États cohérents d'un oscillateur et principe d'incertitude:

3 - Électron et vitesse de la lumière:
La gravité quantique nommée z ferait alors tomber la particule de la surface, pour ensuite réapparaître grâce à l'énergie. Autant la constante g a une accélération sur un objet relativiste, alors z serait une constante d'accélération de la particule quantique pour atteindre la vitesse de la lumière.
Nous pouvons déterminer la quantité d'énergie qu'il faudrait pour déplacer l'électron à c-1:

Énergie potentielle gravitationnelle quantique de l'électron et constante z :

Expliquer la physique quantique avec une seule particule en mouvement.
_
_