4-La gravitation euclidienne

[externo]

Suite des preuves de la véracité de la théorie de Lorentz-Poincaré

On introduit la gravitation comme suit :

En métrique de Minkowski il existe un espace pseudo-euclidien 4D tangent en tout point de la variété pseudo-riemannienne. Cette métrique détermine le temps propre (vieillissement).
Mais on a montré dans l'épisode précédent que la métrique de Minkowski ne définit pas un espace 4D mais seulement un espace 3D+1 et n'est qu'une simple réécriture de la métrique euclidienne 3D+1. Elle n'est qu'un moyen de baliser les distances spatio-temporelles à coup de temps propre, elle n'a aucun pouvoir de changer la géométrie physique telle qu'elle apparaît sur les diagrammes, et cette géométrie est toujours euclidienne. On peut donc remplacer la métrique de Minkowski par la métrique euclidienne. La longueur d'espace-temps n'y est pas le temps propre, voilà tout.

Mais il y a quelque chose de plus fondamental.
1-La gravitation correspond-elle à un espace-temps courbe, que la métrique soit euclidienne ou minkowskienne ?
2-Le passé et le futur coexistent-ils avec le présent (non d'après l'épisode précédent)

A propos du point 2 :
Le monde réel ne contient que le présent vectoriel, le passé et le futur vectoriels n'existent pas, le temps n'est qu'un scalaire et la géométrie physique est celle des quaternions d'Hamilton (ou de l'algèbre de l'espace physique). Néanmoins, on peut très bien représenter graphiquement le passé le futur et le temps sous forme d'un vecteur.

Etude qui montre que l'approche des quaternions fonctionne : https://arxiv.org/pdf/2106.06394.pdf

Voici un dessin où le temps est représenté comme un 4e vecteur de l'espace :
https://i.stack.imgur.com/zmeTI.png
https://askfrance.me/q/pourquoi-la-vite ... 1833726604
https://physics.stackexchange.com/quest ... -spacetime
Sur le dessin le temps est représenté comme une dimension vectorielle pour fixer les idées, il faut imaginer que "l'épaisseur spatiale" du temps représentée sur le dessin n'existe pas. Seul l'espace la possède.

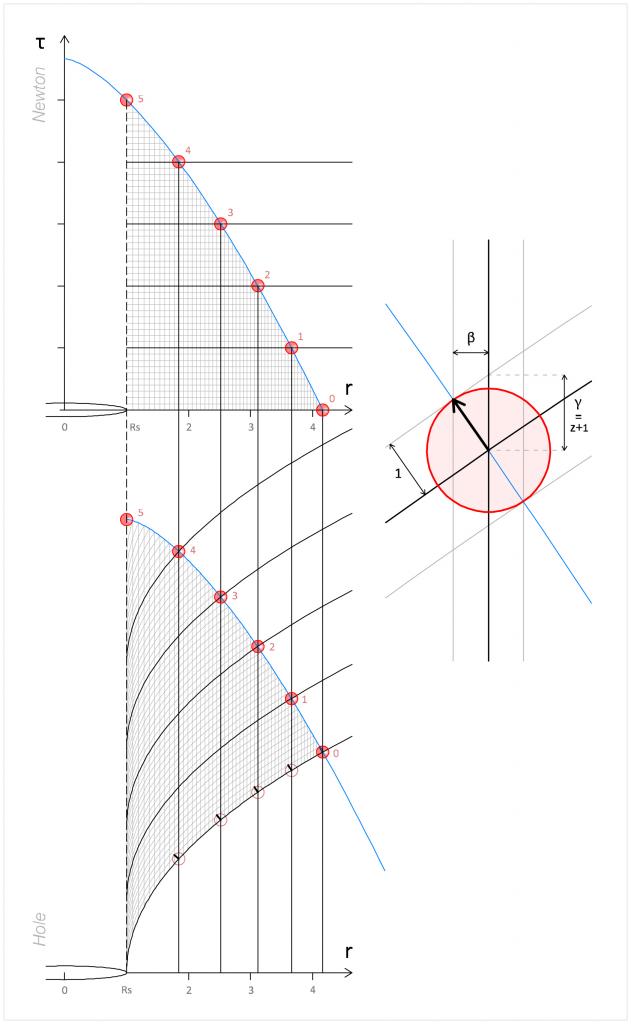
Pour passer de Newton à Einstein il suffit de représenter les trajectoires données par Newton mais en 4 dimensions et donc tenant compte aussi de la courbure espace-espace qui entraîne l'avance du périhélie et le doublement de la courbure de la lumière.
La courbure de l'espace induit une très légère courbure de la trajectoire parcourue par l'objet du fait de sa vitesse initiale, cette courbure n'est pas prise en compte dans les calculs de Newton, qui est une théorie du temps courbe seulement.
Il y a donc deux trajectoires courbes qui concourent à l'orbite spatio-temporelle, une composante temps courbe et une composante espace courbe, la seconde étant plate chez Newton.
Le temps propre ne sert à rien pour tracer la trajectoire des corps.

En outre, on suppose que la gravitation est un espèce d'effet d'ombre, mais plus exactement un effet de réfraction par déformation du matériau de l'espace-temps.

Un modèle gravitationnel de rivière, mais l'auteur adhère à la non existence de l'éther, ce qui est absurde : http://www.alenspage.net/AetherFlowGravitation.htm

Conclusions de cet épisode 4 en tenant compte des acquis des épisodes suivants
[Il faut préciser ici que l'espace de Minkowski comme concaténation de référentiels inertiels n'existe pas et donc que la variété courbe à 4 dimensions vectorielles de la RG non plus.]
La RG modélise un espace courbe à 4 dimensions vectorielles + 1 dimension scalaire. (Algèbre de l'espace-temps)
La théorie des formes différentielle est déficiente, elle passe sous silence la dimension scalaire et on pense donc qu'il n'y a que 4 dimensions. Mais un espace vectoriel courbé nécessite en fait une dimension scalaire de densité pour pouvoir se courber, donc l'espac-temps à 4 vecteurs ne peut être fonctionnel sans une 5e dimension scalaire.
Mais dans l'algèbre de l'espace-temp qui reproduit l'espace-temps de Minkowski il y a bien 4 vecteurs et un scalaire.
Or on peut refaire la RG avec une structure plus petite en 3D +1 qui est l'algèbre de l'espace physique, à condition de reconnaître que seule la métrique de Painlevé correspond au point de vue physique (lumière isotrope du chuteur).

Quand on définit les symboles de Christoffell on déforme des petits carrés d'espace-temps. On change les angles et les échelles pour produire une courbure. Les angles ce sont les dimensions d'espaces qui pivotent les unes dans les autres, le changement d'échelle c'est la dimension scalaire qui le prend en charge.
Donc l'espace-temps 4D se courbe à l'aide d'une 5e dimension scalaire, appelée w quand on la représente.
Dans ce cas la forme de Schwarzschild vaut celle de Painlevé, il n'y a pas de vrai découpage, l'espace-temps est courbé dans w. Donc quel que soit le mixage entre le temps et l'espace on peut toujours le négliger, considérer que ce ne sont que des changements de repères et que la vraie courbure est dans w et implique les 4 dimensions en même temps. Voilà pour l'interprétation de la physique mainstream.

Mais si on comprend qu'il existe un seul découpage physique entre temps et espace, que le temps n'est pas un vecteur mais un scalaire, car il est impossible de se promener dans le temps comme on se promène dans l'espace, nous n'avons pas besoin de dimension w, c'est le temps qui joue ce rôle, c'est lui qui est responsable des changements d'échelles (divergences). Ainsi la forme de Schwarzschild est un point de vue à temps constant donc c'est une carte où il manque la dimension de la profondeur temporelle dans laquelle l'espace s'incurve.

Différence entre métrique 4D de Minkowski et euclidienne.

La métrique euclidienne permet de gérer un découpage comme un espace-temps à 4 dimensions.
La métrique de Minkowski balise l'espace-temps à coup de temps propre mais n'a pas le pouvoir de changer la géométrie. La métrique de Minkowski qui gère tous les référentiels comme s'ils étaient réels, espèce de concaténation de tous les éthers possibles, n'existe pas (vu à la fin de l'épisode précédent).
On voit en quoi elle est déficiente : elle duplique les objets dans un univers-bloc. Normalement, quel que soit le référentiel, on doit observer le même objet avec les mêmes dimensions : elle n'observe pas des objets mais des lignes d'univers, depuis un référentiel on observe l'objet à telle époque et depuis un autre à tel autre époque. Il n'y a pas unicité des objets physiques, en quelque sorte les objets individuels n'existent pas. C'est ce que corrige la métrique euclidienne. La première chose à comprendre est que le décalage de temps entre l'avant et l'arrière de l'objet est un décalage de temps dans le référentiel de l'éther. En métrique de Minkowski les deux extrémités sont à la même époque pour l'observateur mais pas pour l'objet, alors qu'en métrique euclidienne l'objet est asynchrone par rapport à l'éther, et c'est un fait absolu qui représente une longueur de temps. Du point de vue de l'objet, c'est l'éther qui est asynchrone, parce que ses axes de temps ont subi une rotation d'angle θ tel que 1/γ = cos θ et β = sin θ, mais c'est une illusion. Cette rotation c'est l'objet qui l'a subi, il a subi une déformation par divergence. L'opérateur divergence représente une rotation de l'espace dans le temps de même que le rotationnel représente une rotation entre les dimensions spatiales.
Il se passe la même chose en relativité générale, et ce sont ces déformations qui sont à l'origine de la courbure de l'espace-temps. En RR les objets sont en mouvement dans un espace-temps localement plat ce qui les place en situation d'anisotropie par rapport à lumière (en fait par rapport aux ondes quantiques de l'éther dont ils sont constitués) ; en RG c'est la lumière (et les ondes) qui est anisotrope par rapport à l'espace, ce qui impose cette fois une contraction de tout l'espace, qui est une rotation dans la dimension du temps (divergence, partie newtonienne) et une rotation des axes spatiaux (rotationnel, courbure spatiale non présente chez Newton) en raison de la symétrie sphérique.

En fin de compte, la métrique euclidienne avec temps scalaire est une réalité tandis que la métrique de minkowski avec temps vectoriel est une illusion.

Equivalence géométrique entre la RR et la RG

L'idée que l'objet en mouvement change de simultanéité et effectue une rotation dans l'espace-temps est bonne, ce qui est mauvais c'est de croire que c'est atteignable par une nouvelle simultanéité qui restaure l'isotropie de la lumière. Pour cela nous avons besoin d'un univers-bloc dans lequel le passé, le présent et le futur coexistent. En réalité, l'isotropie est perdue et il ne faut pas chercher à la retrouver, il faut au contraire acter qu'elle est perdue. Il faut basculer euclidiennement les axes d'espace-temps de sorte qu'ils restent isotropes d'un cône de lumière virtuel qui accélèrerait avec l'objet comme en métrique de Painlevé avec le chuteur, sauf qu'ici le cône ne bouge pas. L'objet en mouvement possède donc une simultanéité qui n'est pas la simultanéité physique de la lumière et n'est donc pas simultanée, ce n'est donc pas une simultanéité mais plutôt un axe spatial asynchrone.

Donc au bout du compte la simultanéité lorentzienne est effectivement factice mais cela n'empêche pas qu'il existe pour tous les objets mouvants un axe spatial qui leur est propre et par rapport auquel la lumière n'est pas isotrope. Il s'obtient par rotation euclidienne de l'axe spatial de l'éther. L'angle dépend de la vitesse tel que le sinus de cet angle vaut v/c. C'est l'angle d'aberration. C'est exactement le même angle que l'on retrouve en relativité générale car 1-Rs/R vaut le carré de ce sinus. L'espace-temps est donc euclidien, ce qui différentie le temps de l'espace ce n'est pas la signature, mais le fait que c'est une dimension scalaire (densité).
https://forum-sceptique.com/viewtopic.p ... &start=175

Cours :
http://www.blau.itp.unibe.ch/newlecturesGR.pdf
https://arxiv.org/pdf/gr-qc/9712019
https://liphy-annuaire.univ-grenoble-al ... ometry.pdf

Texte de Lorentz écrit en français en 1914, qui explique la RG dans le cadre de l'éther :
https://www.lorentz.leidenuniv.nl/IL-pu ... S_1914.pdf

Voici des représentations correctes de la déformation de l'éther :
https://64.media.tumblr.com/659da12fac7 ... 1_500.gifv


Simulation des trajectoires en 2D :

[externo]

Proposition de géométrie

Un fil Futura sur le sujet :

https://forums.futura-sciences.com/astr ... dence.html

La tangente au paraboloïde est l'axe d'espace du chuteur. L'orthogonalité constatée dans le fil est celle entre l'axe du temps et l'axe d'espace du chuteur.
Les immobiles sont contractés et leur temps est dilaté conformément à la théorie de l'éther de Lorentz par leur mouvement dans l'espace local à la vitesse de libération (la vitesse de la lumière est anisotrope).

Voir ce fil du forum physique-online où il est finalement compris que la dimension du temps est une dimension comme les autres et que la chronogéométrie est une erreur. Le temps et le vieillissement sont deux choses différentes :
http://www.
forum2.math.ulg.ac.be/viewthread.html?SESSID=45d674e9693612a6a593f0bfb1c3fb14&id=13703

Arc.png

En rouge la ligne d'univers du chuteur qui est aussi l'axe du temps local. Les paraboles vertes, jaune et bleues représentent trois instants absolus différents. Ces paraboles sont inclinées à 45° au niveau de l'horizon et à 90° au niveau de la singularité. Il ne s'agit donc pas du paraboloïde de Flamm, qui est incliné à 90° au niveau de l'horizon pour modéliser la contraction infinie de la matière en ce point.
L'énergie du vide glisse peu à peu vers le bas mais se renouvelle perpétuellement par en haut en venant de l'infini et la ligne du présent reste identique à elle-même quand on la fait évoluer dans le temps d'univers.
Ainsi ce n'est pas l'espace qui glisse mais l'énergie qu'il contient.

Voir un meilleur graphe ici :

https://forums.futura-sciences.com/astr ... nce-2.html
post 46 (ajout 10/10/2022)
Réexplicitions plus détaillées :
La trajectoire bleue de chute libre représente la ligne d'univers du chuteur.
La courbe qui lui est orthogonale représente la surface de l'univers qui à cet endroit est incurvé par la gravitation.
Il faut bien voir cette surface comme une substance palpable et pliable en 3 dimensions, l'éther, le vide, etc... et non pas comme "rien".
En ordonnée sur le schéma il faut placer le temps cosmique, c'est à dire le temps en espace plat à l'infini.
La lumière se déplace à tout instant à égale distance entre la tangente à la courbe du temps bleu du chuteur et la tangente au parabole car sa trajectoire doit toujours être à 45° entre les axes de temps et d'espace locaux.

Il y a orthogonalité entre la trajectoire de Newton avec le temps coordonnée de l'infini (t) en ordonnée et la ligne d'espace (qui est à 45° sur l'horizon et 90° sur la singularité).
En fait, le chuteur de Painlevé dépasse la vitesse de la lumière (45°) sur l'horizon même du point de vue de l'éloigné. C'est comme en cosmologie : la vitesse de la lumière n'est pas une limite parce qu'il ne s'agit pas de mouvements dans l'espace mais de mouvements de l'espace. Par contre, ici, en raison de la différence physique des situations (absence d'expansion entre la lumière et l'éloigné), la lumière ne parvient jamais aux yeux de l'éloigné.
La vitesse de chute dépend simplement de l'angle de l'axe du temps. Le déplacement temporel préexistant dirigé verticalement à la vitesse c déteint dans l'espace de l'éloigné.
L'axe d'espace fait toujours 90° avec l'axe du temps. C'est d'ailleurs sa variation qui est à l'origine de la variation de l'axe du temps. La prise en compte de la variation de l'axe d'espace autour du trou noir (courbure) en plus de la variation de l'axe du temps permet de prévoir le doublement de la courbure de la lumière et l'avancée du périhélie.

Voici une vidéo qui représente à peu près correctement la géométrie de l'espace-temps en champ de gravitation :

Il y manque toutefois le mouvement de l'espace dans le temps d'univers et l'aberration conséquente du cône de lumière.

Voici une représentation en diagramme de Minkowski

Géométrie gravitation.png

Pour résumer :

Cette géométrie est-elle correcte ?
Non. Voir plus loin.
En réalité l'angle fait 90° sur l'horizon.

------------------

Une rivière est constituée de gouttelettes en mouvement, mais la forme de la rivière ne change pas alors que les gouttelettes sont mobiles. La forme de la rivière peut être une courbe, une boucle. La rivière c'est l'énergie gravitationnelle et sa forme c'est l'espace. L'espace peut donc être courbe.
Dans un espace plat, l'énergie est stationnaire (hormis les fluctuations) et la rivière n'a aucun courant spatial, c'est un lac. Mais dans le schéma Hole le courant se fait sentir et l'espace se courbe en raison de la mise en mouvement de l'énergie. L'éther est en tension, transmettant l'énergie qui suit donc la courbe de Newton. En approchant du trou noir le courant l'énergie accélère et le changement de direction s'accentue, il atteint 45° ou 90° sur l'horizon. L'énergie descend le long de la rivière mais pendant ce temps la rivière se renouvelle en amont en raison de l'attraction gravitationnelle, faisant que la rivière en se renouvelant reste de niveau avec le lac et s'élève avec lui dans le temps coordonnée de l'infini (temps cosmique).

Mécanisme géométrique de la gravitationnel :
(contient des explications avancées issues des épisodes 5 et 6)
Il n'y a aucune différence intrinsèque entre les 3 dimensions d'espace et la dimension du temps. Simplement il y a 3 degrés de liberté pour 4 chiffres, le 3, le 2, le 1 et le 0. La dimension associée au 0 n'a aucun degré de liberté, c'est la dimension scalaire qui gère le facteur d'échelle.
Les dimensions ont la propriété de pouvoir s'interchanger, dans la rotation de Kerr les dimension d'espace s'inversent. Ce phénomène se produit aussi avec la dimension 0, et c'est là que nous avons les phénomènes relativistes de contraction des longueurs, dilatation du temps et changement de simultanéité. Dans un champ de gravitation il y a un tel basculement entre la dimension du temps (normalement orthogonale) et la dimension radiale de l'espace, ce qui fait que l'espace bascule dans ce qui est du point de vue extérieur le temps et se contracte parce qu'il s'y rajoute partiellement une longueur de temps. C'est ce qui permet à l'espace de se courber, c'est comme s'il se courbait dans une 4e dimension vectorielle, sauf qu'il n'y a pas de vecteur. C'est donc la même chose que la courbure riemannienne, sauf que Riemann l'a traité autrement, en se passant de l'idée d'une dimension supplémentaire. Or cette dimension existe bien et sert à calculer les longueurs, mais elle n'a aucun degré de liberté. Donc l'image du drap tendu est la réalité, ce sont les dimensions d'espace qui s'intervertissent avec cette dimension scalaire. Avec cette métrique bien sûr l'élément de longueur n'est pas le temps propre, parce que les référentiels ne sont pas équivalents. Dans le référentiel de l'éther, les objets immobiles ont un déplacement dans la direction du temps, les objets en mouvement on en plus un déplacement spatial et les deux s'ajoutent. Les objets au repos ont leur extrémité à la même coordonnée temporelle, mais les objets en mouvement non, car leur mouvement vient de ce que l'espace s'est en partie mélangé avec le temps par rotation euclidienne et leur longueur vaut longueur contracté ² + décalage de temps ² ; c'est leur longueur propre et elle se conserve par changement de référentiel. C'est une vue en perspective parce que l'objet est comme orienté vers le passé. Il n'est donc plus dans le référentiel de l'éther, il n'est plus synchrone.

Dans un champ de gravitation l'axe du temps s'incline, mais cependant l'éther continue de progresser dans la même direction que hors du champ de gravitation (verticalement), son référentiel n'est plus isotrope par rapport à la lumière, la lumière est isotrope dans le référentiel du chuteur. Cela vient de ce que les échanges d'énergie au sein de l'éther ne sont plus nuls. Les ondes dirigées vers la masse vont plus vite que dans l'autre sens. Ainsi la coordonnée de temps s'égrène moins vite et il y a une progression de la coordonnée d'espace (dimension vectorielle) : l'éther est en mouvement vectoriel, comme les immobiles. L'éther n'est donc plus synchrone, comme un objet en mouvement en RR. Les chuteurs de l'infini par contre ont leur coordonnée de temps qui évolue seule et n'éprouvent pas la dilatation du temps, ils se laissent entraîner par l'énergie et la lumière reste isotrope par rapport à eux. Donc on peut dire que le chuteur est immobile et l'éther en mouvement, mais c'est local, par rapport au CMB l'éther est toujours immobile (sauf les oscillations pour transmettre le mouvement)

On peut utiliser la métrique dL² = dt²+dx²
A chaque évènement (t, x) correspond la longueur dt²+dx² en métrique euclidienne.

Faux, reliquat d'un point de vue transitoire laissé ici pour référence :
En métrique euclidienne Tau n'est pas représenté géométriquement, et c'est normal car tau n'est pas le vrai temps mais un temps local conséquence de l'anisotropie locale de la vitesse de la lumière. Les processus physiques sont ralentis comme une horloge de lumière (en fait comme des ondes stationnaires en mouvement) donc il ne faut attribuer aucune réalité géométrique à tau.
Einstein a voulu a toute force que les référentiels galiléens soient équivalents, or ils ne le sont pas car la vitesse de la lumière n'est pas la même relativement à chacun d'eux. Dans un seul et unique référentiel la lumière est localement isotrope.

En RG, les objets plus ou moins immobiles dans un champ de gravitation sont dans un environnement où la lumière n'est pas isotrope et subissent donc un "vent d'éther" qui les contractent et dilatent. En fait l'énergie ondulatoire enfermée dans la matière et qui fait sa masse ne peut pas se propager symétriquement dans un mouvement de va et vient stationnaire à la vitesse de la lumière, car elle est elle-même en mouvement par rapport à son milieu de propagation. C'est la mécanique des ondes qui pilote la contraction des longueurs et la dilatation du temps. En RR et en RG ces phénomènes ont exactement la même origine : le "vent d'éther."

Bien entendu, la lumière accélère (vitesse >c) quand elle tombe dans la gravitation et elle accélère (vitesse <c) quand elle en sort. Plus exactement, c'est son support (les ondes de l'éther) qui se déplace.
De même qu'en RR avec l'effet Sagnac, autour des trous noirs de Kerr on peut mettre en évidence la variation de la lumière : la lumière est accélérée dans le sens de rotation de l'espace et ralentie dans l'autre sens.


Sur ce schéma,
https://en.wikipedia.org/wiki/Bell%27s_ ... orizon.svg
on peut voir les lignes d'univers de l'avant et de l'arrière d'une objet qui accélère.
La ligne horizontale correspond au référentiel de départ que l'on peut assimiler à celui de l'éther. Il existe un référentiel dans laquelle la fusée conserve sa longueur propre et où la vitesse de la lumière est isotrope, on le trouve par le changement de simultanéité. Les lignes vertes et rouges correspondent aux lignes de simultanéité de l'arrière et de l'avant de la fusée. Si on utilise la métrique de Minkowski on trouve que la longueur de la fusée reste invariante.

Effet Shapiro radial.

On sait en RR qu'un rayon de lumière met gamma² fois plus de temps pour faire un aller-retour dans le sens du mouvement le long d'un objet se déplaçant à la vitesse v associée au facteur gamma, et que cette durée est réduite à gamma en raison de la contraction de la longueur de l'objet elle-même de gamma.
L'effet shapiro radial est identique à la différence qu'il n'y a pas contraction des longueurs puisque la lumière épouse la courbure temps/espace radiale. La lumière est donc plus lente d'un facteur gamma² sur l'aller-retour.

Shapiro radial.png

Les traits rouges représentent le cône de lumière incliné vers la droite. La lumière est accélérée vers la droite et ralentie vers la gauche.
Sur ce dessin l'accélération "gravitationnelle" n'obéit pas à la loi de Newton, la vitesse augmente de 0 à l'infini le long du quart de cercle.
Dans un vrai champ gravitationnel la courbure n'est pas un arc de cercle mais le principe est le même.
Ce diagramme est un diagramme de Minkowski ou de Newton. Angle de trajectoire = 0 = vitesse nulle, angle = 90° = vitesse infinie.
La lumière rouge qui va vers la droite est accélérée par rapport à l'éloigné : dr/dt > 1
Comme la lumière rouge allant à droite se dirige dans une direction différente de la lumière jaune allanr à droite, du point de vue de l'éloigné elle semble descendre en suivant un arc de cercle. Au fur et à mesure qu'elle descend elle tourne et accélère : elle descend le puits gravitationnel tout en accélérant du point de vue de l'éloigné. Mais en fait, elle ne fait que changer de direction en suivant la courbure du cercle.
Les lignes rouges sont les lignes d'univers de la lumière, c'est la "géodésique" de genre temps. Ces lignes se courbent en descendant le cercle mais ce n'est pas représenté sur le dessin, qui ne donne que la trajectoire instantanée.
L'arc de cercle correspond à la simultanéité absolue, c'est pour cela que les deux "t" sont sur le cercle.
N'est pas représenté non plus sur le dessin le fait que l'ensemble est emporté verticalement par le temps coordonné, mais ça a pour conséquence que le cercle représenté est fictif et que l'espace physique reste plat, contrairement à la sphère cosmique où il s'incurve.

La dilatation du temps et contraction des longueurs s'expliquent par la variation de la vitesse de la lumière par rapport à un référnetiel absolu. Sur le dessin il y a une petite flèche bleue sur le cercle. C'est la ligne d'univers d'un immobile. Placé à cet endroit il subit une forte dissymétrie de la vitesse de la lumière qui cause sa contraction et dilatation.
La RG peut donc être représentée comme un diagramme d'espace-temps incliné.

RR :
La vitesse de la lumière n'est pas la même dans deux référentiels galiléens différents.
On peut faire comme si c'était la même, à condition de resynchroniser les horloges. L'anisotropie naturelle de la vitesse de la lumière est alors annulée.
Il est normal que dans les référentiel en mouvement la longueur propre se conserve puisque ces référentiels simulent qu'ils sont dans le référentiel de l'éther.
La synchronisation d'Einstein permet de resynchroniser des processus que la vitesse a désynchronisés et ça permet de conserver les mêmes lois pour tous les référentiels. Ca permet aussi de faire des calculs simplement sur les durées.

Coordonnées de Schwarzschild :
Même méthode. L'anisotropie de la vitesse de la lumière dans le champ de gravitation est remplacée par un changement de simultanéité induit par la courbure de l'espace-temps. Comme les objets ne se déplacent pas c'est que le changement de simultanéité vient de l'espace lui-même.

Quand un objet immobile dans le champ synchronise ses deux extrémités celles-ci ne sont pas synchronisées, celle qui est plus en bas dans le champ est en avance sur celle qui est plus en haut du point de vue de l'observateur éloigné.
La lumière qui fait un aller-retour de l'éloigné vers un immobile met en métrique de Schwarzschild standard la même durée pour l'aller que pour le retour. En réalité, le trajet d'aller est plus court que celui de retour, donc l'heure indiquée par l'immobile et portée par la lumière qui revient vers l'éloigné a été indiquée plus tôt que ce que nous disent les coordonnées de Schwarzschild. C'est parce que ces coordonnées, en supprimant l'anisotropie de c, ont en même temps supprimé le décalage des heures introduit par la synchronisation d'Einstein.
C'est la même chose pour le chuteur, qui est arrivé sur le point où la lumière le rattrape bien avant ce que nous disent les coordonnées de Schwarzschild. Donc même si la lumière qui le rattrape sur l'horizon ne remonte jamais jusqu'à l'éloigné, elle le rattrape assez vite et le chuteur passe bien l'horizon du point de vue de l'éloigné aussi.
La métrique de Schwarzschild encode la contraction des longueurs et la dilatation du temps gravitationnels dans la métrique mais ne leur donne pas pour origine l'anisotropie de la vitesse de la lumière.

Plus on s'enfonce dans le puits plus les horloges immobiles qui marquent la même heure sont décalées dans le futur de l'éloigné. Si bien que si un immobile se met à chuter, partout où il passera l'heure que son horloge marquera ne sera différente de l'heure locale qu'en raison de la dilatation temporelle (apparente ou réelle) due au mouvement. Sa dilatation temporelle gravitationnelle sera simulée par le décalage initial. On aura l'impression que son temps à lui aussi est ralenti par la gravitation, parce que le fait que son horloge tourne plus vite que celle de son environnement sera masqué par le décalage initial qui compensera exactement.
Donc si un chuteur démarre de loin, bien que son temps reste toujours synchrone avec le point d'où il démarre, il semble malgré tout subir la dilatation du temps.

Schéma avec explications

L'image ci-dessous représente schématiquement la courbure gravitationnelle. Sur l'horizon elle atteint un angle de 90°, la vitesse de la lumière mesurée par rapport à l'observateur éloigné est de 0 en sortie et 2c en entrée. Comme la ligne d'univers de l'espace est partout verticale la vitesse de la lumière n'est pas isotrope et le chuteur n'est pas immobile : L'espace est anisotrope.

Géométrie cosmos.png

Dans la représentation que l'on trouve de la géométrie de Painlevé l'espace reste radialement plat :
https://commons.wikimedia.org/wiki/File ... iagram.png
Si l'éther était mobile il serait courbé dans le plongement du paraboloide et la représentation changerait :
1-On voit que l'axe r est horizontal et que la ligne d'univers du chuteur sur l'horizon est de 45°. Il faudrait abaisser cette ligne d'univers de 45° ainsi que le cône de lumière et donc elle n'atteindrait plus à la même hauteur, elle serait en contrebas par rapport à la ligne du présent de l'observateur éloigné.
2-L'axe r devrait en outre s'incurver et s'incliner d'un angle de 90° sur l'horizon et non demeurer éternellement horizontal.

Il est vrai que cette représentation ne figure pas le paraboloïde de Flamm et la plongée dans le temps coordonnées, mais physiquement dans le champ l'espace n'est pas courbe radialement, il est contracté, et cette représentation figure bien un espace contracté. S'il était en chute libre, la géométrie serait celle de la sphère cosmique.

https://forum-sceptique.com/viewtopic.p ... 31#p647631


Le message suivant est ici

[bongo]

Et je prétends que la métrique de Minkowski ne sert strictement à rien pour modéliser un champ gravitationnel.

Tu as entièrement raison !! L'espace-temps de Minkowski est dénué de courbure et donc ne peut prétendre décrire la gravitation.

D'ailleurs elle ne prétend pas décrire la gravitation, puisqu'elle ne décrit pas la gravitation. Elle est née en 1907, quand Minkowski a vu que les objets manipulés par Einstein étaient en fait des objets quadridimensionnels, des quadrivecteur évoluant dans un espace pseudo-euclidien.

Einstein a ensuite reprise ce formalisme et a montré qu'il fallait rajouter de la courbure pour pouvoir décrire la gravitation : un espace de Riemann.

[externo]

Et bien je dis qu'il n'y a pas besoin de rajouter de la courbure à un espace-temps de Minkowski pour décrire la gravitation, il suffit de la rajouter à un espace-temps euclidien. Mais attention, il n'est pas question de courber l'espace-temps 4D euclidien dans une dimension virtuelle.

[bongo]

Tu peux dire ce que tu veux. Après écris-moi ton calcul pour la déviation des rayons lumineux

[externo]

Prenons le problème autrement : sais-tu que la théorie de l'éther de Lorentz est équivalente à la théorie de la relativité restreinte d'Einstein mais n'a pas besoin de l'espace-temps de Minkowski pour reproduire les mêmes résultats ?